kkaya
1
初めて質問させていただきます。
二足歩行ロボットの制御シミュレーションをChoreonoidを用いて行っています。その際、運動方程式内の慣性行列Mを取得する必要があるのですが、calcMassMatrix関数を用いて値を取得した場合、転置で同一になるような形で出力されませんでした。
浮遊リンク系をモデル化した場合、以下の論文(7-19式)のように、転置で同一になる形で出力されると考えていましたが、空間速度ベクトルを用いているため、従来の加速度、角加速度とは異なる形で慣性行列Mが出力されるのでしょうか。
それとも他にやり方があるのでしょうか。
参考:吉田 和哉, The SpaceDyn: ダイナミクズ計算のためのMATLABツールボックス
[The SpaceDyn: ダイナミクズ計算のためのMATLABツールボックス]
ご回答いただけると幸いです。よろしくお願いいたします。
実際の出力される行列と,ソースコードを載せていただくことはできますか?
こちらでも検証します.
kkaya
3
返信ありがとうございます。
実際にやりたいことは、各制御ループ内で慣性行列を取得することになります。
Simpleコントローラとして実装したコードを下記に添付いたします。
また、実際に使ったモデル(簡単のため、SR1モデルから上体を取り除いたモデル)のBODYファイルも添付いたします。
MyController.zip (1.1 KB)
SR1.body (7.3 KB)
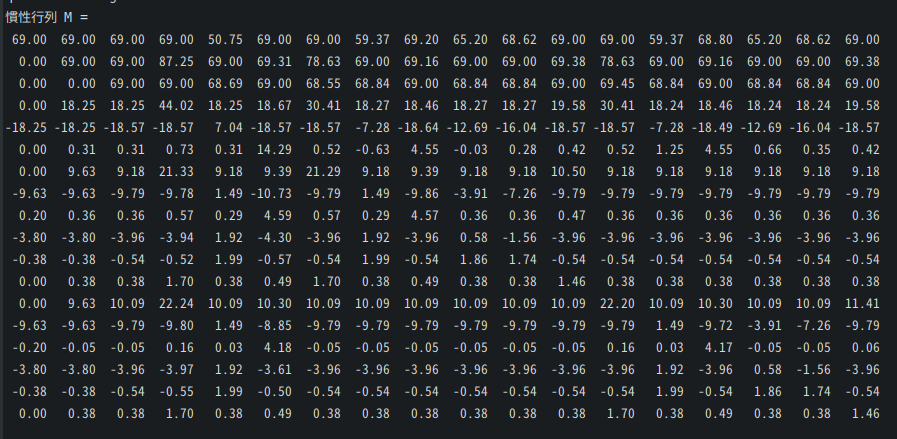
実際に1ループ目で出力された慣性行列は以下の18×18行列になります。
よろしくお願いいたします。
ソースコードを拝見しました,こちらで試した結果同じ現象が確認できました.
実験的な回答で恐縮なのですが,下記の二重for文を追加実装することで慣性行列を算出できました.
//慣性行列の計算
calcMassMatrix(robot, MM);
for(uint8_t i = 1; i < MM.cols(); i++) {
for(uint8_t j = 0; j < i && j < 3; j++) {
MM.col(i) -= MM.col(j);
}
}
cout << "慣性行列 M =" << endl;
cout << std::setprecision(2) << MM << endl;
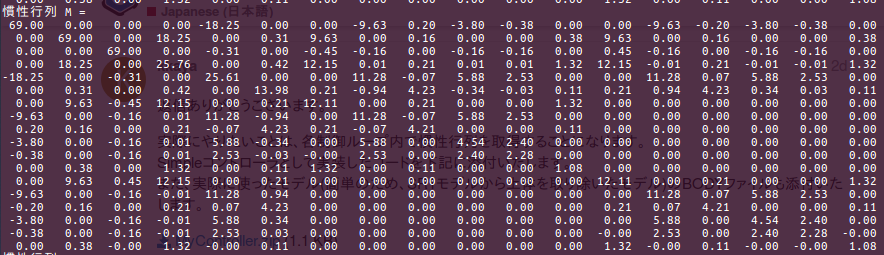
今回観測されたバグ(?)としては,慣性行列の重心並進に対応する列 (0~2列目) が以降の列に全て加算されているようでした.
これを取り除いたところ,対称性のある,物理的にも無理のない値が出てきました.
(画像で添付します)
まだ内部実装を追いきれていないのですが,取り急ぎご確認いただければと思います.
nakaoka
6
kkaya様、不具合のご指摘ありがとうございます。
そしてYuki_Onishi様、修正方法について調査・提示いただき誠にありがとうございます。
こちらでも確認して修正を取り込みたいと思います。
(ただすみません、今会社の業務で立て込んでおりまして、今しばらくお待ちいただけますでしょうか。よろしくお願い致します。)
本件対応が大変遅くなりまして申し訳ありません。
バグの方修正してコミットしておきました。
kkaya さんのサンプルについても正常な値が出力されることを確認しました。
なお、この関数は以前はBodyヘッダをインクルードすると使えていましたが、必ずしもBodyクラスと同時に使うものではないため、Bodyヘッダに含めるのは見直しました。MassMatrixというヘッダがありますので、
#include <cnoid/MassMatrix>
としてお使いください。
バグの原因としては、単位ベクトル法で各加速度要素を順番に1にしていく中で、ルートリンクの並進要素に関して0に戻し忘れている部分がありました。単純なコーディングミスです。
Yuki_Onishi さんの調査・報告のおかげでこのバグをみつけることができました。ありがとうございました。
2 Likes
nakaoka
8
calcMassMatrix関数について、直したついでに必要な計算まで除去してしまっていたことに気がついたので、再度修正しておきました。
1 Like
初めまして、
先にGithubにIssueを立ててしまったのですが、その後にdiscouseの方が活発に議論が行われているとのことを知ったため、こちらでも質問させていただきます。
calcMassMatrix関数を用いた慣性行列計算において、rotorInertiaが2回足されているように思います。まず、
の中でやっている逆動力学演算A_G * delta_i + b_G (梶田先生教科書第2版6.40式)
で、rotorInertiaを含んだ形でA_G * delta_i + b_G を計算しています。その後、
で、A_G * delta_i + b_G のi成分にさらにrotorInertiaを足しています。
順動力学計算コード
あたりを眺めると、慣性行列にrotorInertiaを1回足す方が順動力学計算結果と整合性が取れるように思うのですが、いかがでしょうか?
nakaoka
10
ご指摘ありがとうございます。
確かにご指摘の内容で間違いないように思います。コードに誤りがありまして申し訳ありません。
修正としては、以下の行を削除すればよさそうですね。
こちら対応してコミットしたいと思います。
ご協力ありがとうございました。
1 Like